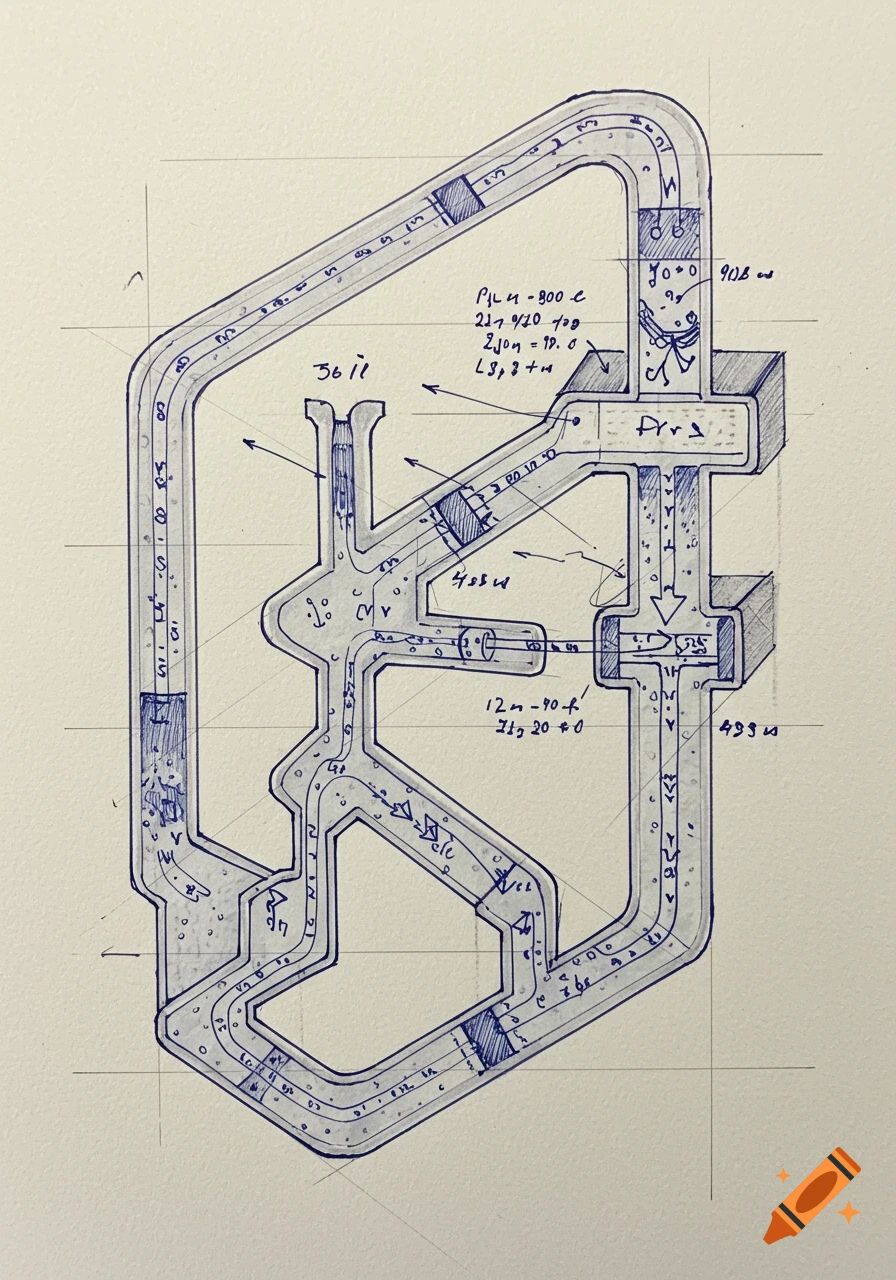
A sepia-toned sketch shows a roller coaster track forming a 5th-degree polynomial graph, with a 250ft height marked.

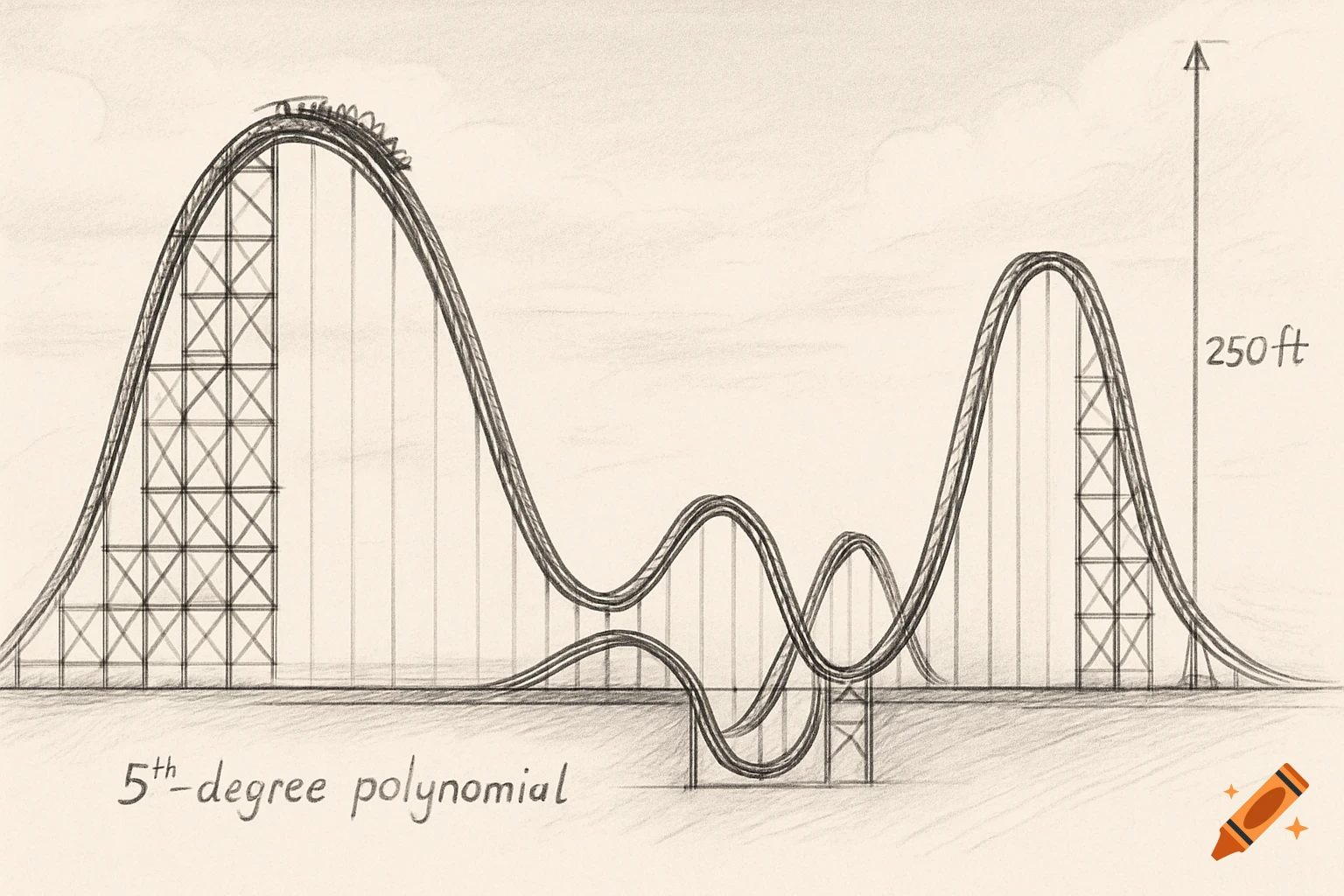
1. Sketch and basic ideaFor my roller coaster design, I created a polynomial graph that starts at a high point, drops down below ground once, and then comes back up to end at 250 feet, like the instructions say. The graph has several hills and valleys so the ride looks exciting but still realistic.2. Zeros (roots) of the polynomialThe zeros of my polynomial are the x‑values where the coaster is at ground level (height 0). These roots show all the times during the ride when the coaster touches the ground or enters/exits the tunnel.(Here you would list them, for example: [x = -2, 1, 4, 4, 6 + 2i, 6 - 2i].)3. Factored formUsing those zeros, the polynomial in factored form is:The double root shows where the track just “touches” the ground and turns around instead of crossing through it.4. Standard form of the equationAfter multiplying out the factors (and choosing a value for [a] so the ending height is 250 feet), the polynomial can be written in standard form:(Here you would actually write the full expanded equation from your work.)5. Verifying the equationTo check that the equation is correct, synthetic or long division can be used with each zero. If each factor divides evenly with no remainder, that confirms the polynomial matches the roots from the graph.6. End behaviorBecause this is a 5th‑degree polynomial with a positive leading coefficient, as [x \to -\infty], [f(x) \to -\infty], and as [x \to \infty], [f(x) \to \infty]. This means the left side of the graph goes down See more